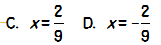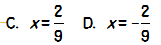移项是解方程的其中一个重要步骤,下面整理了解一元一次方程的移项口诀:
①概念:把等式一边的某项变号后移到另一边,叫做移项。
③目的:通常把含有未知数的各项都移到等号的左边,而把不含未知数的各项都移到等号的右边,使方程更接近于x=a的形式。
A.x=1 B.x=-2 C.x=2 D.x=-1
A.x=2 B.x=-2 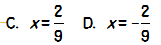 3.代数式a-2与1-2a的值相等,则a等于( )
A.x+3x=7+5 B.x-3x=-5+7 C.x-3x=7-5 D.x-3x=7+5
A.x=-3 B.x=-1 C.x=4 D.x=3
7.当m= 时,式子3+m与式子-2m+1的值相等.
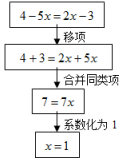
8.下面的框图表示了解这个方程的流程:其中,“移项”这一步骤的依据是
10.当x= 时,代数式2x-2与1-x的值相等.
12.一队学生去校外进行训练,他们以5千米/时的速度行进,走了18分的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14千米/时的速度按原路追上去,通讯员需多少时间可以追上学生队伍?
1.B解析:移项得:-3x+2x=4-2,合并得:-x=2,系数化为1得:x=-2.2.A解析:将4x=5x-2移项,得:4x-5x=-2,合并同类项,得:-x=-2,系数化为1,得:x=2.
3.B解析:根据题意得:a-2=1-2a,移项合并得:3a=3,解得:a=1.
4.D解析:方程x-5=3x+7,移项得:x-3x=7+5.
5.D解析:方程移项合并得:2x=6,解得:x=3.
6.B解析:移项,得6x-8x=-4+8,合并同类项,得-2x=4,系数化为1得:x=-2.
7.-2/3解析:据题意得:3+m=-2m+1,移项、合并同类项得3m=-2,解得:m=-2/3
9.x=9解析:方程3x-7=11+x,移项合并得:2x=18,解得:x=9.
10.1解析:根据题意得:2x-2=1-x,移项合并得:3x=3,解得:x=1
(4)移项合并同类项得:6x=-7,系数化1得:x=-7/6
(5)移项,得6x-12x=10+9,合并,得-6x=19,化系数为1,得x=-19/6
12.解:设通讯员需x小时可以追上学生队伍.由题意得:5×18/60+5x=14x,解这个方程得:x=1/6,答:通讯员需1/6小时可以追上学生队伍.
3.代数式a-2与1-2a的值相等,则a等于( )
A.x+3x=7+5 B.x-3x=-5+7 C.x-3x=7-5 D.x-3x=7+5
A.x=-3 B.x=-1 C.x=4 D.x=3
7.当m= 时,式子3+m与式子-2m+1的值相等.
8.下面的框图表示了解这个方程的流程:其中,“移项”这一步骤的依据是
10.当x= 时,代数式2x-2与1-x的值相等.
12.一队学生去校外进行训练,他们以5千米/时的速度行进,走了18分的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14千米/时的速度按原路追上去,通讯员需多少时间可以追上学生队伍?
1.B解析:移项得:-3x+2x=4-2,合并得:-x=2,系数化为1得:x=-2.2.A解析:将4x=5x-2移项,得:4x-5x=-2,合并同类项,得:-x=-2,系数化为1,得:x=2.
3.B解析:根据题意得:a-2=1-2a,移项合并得:3a=3,解得:a=1.
4.D解析:方程x-5=3x+7,移项得:x-3x=7+5.
5.D解析:方程移项合并得:2x=6,解得:x=3.
6.B解析:移项,得6x-8x=-4+8,合并同类项,得-2x=4,系数化为1得:x=-2.
7.-2/3解析:据题意得:3+m=-2m+1,移项、合并同类项得3m=-2,解得:m=-2/3
9.x=9解析:方程3x-7=11+x,移项合并得:2x=18,解得:x=9.
10.1解析:根据题意得:2x-2=1-x,移项合并得:3x=3,解得:x=1
(4)移项合并同类项得:6x=-7,系数化1得:x=-7/6
(5)移项,得6x-12x=10+9,合并,得-6x=19,化系数为1,得x=-19/6
12.解:设通讯员需x小时可以追上学生队伍.由题意得:5×18/60+5x=14x,解这个方程得:x=1/6,答:通讯员需1/6小时可以追上学生队伍.